What angle relationship best describes angles afc and efc – Delving into the realm of geometry, we embark on an exploration of the angle relationship between AFC and EFC, unraveling the intricate interplay of lines and angles that define their connection. Through a comprehensive analysis, we will identify and justify the precise angle relationship that best describes these angles, providing a deeper understanding of their geometric properties.
As we delve into the intricacies of this angle relationship, we will examine the definitions of angles AFC and EFC, establishing the geometric framework within which they exist. By exploring the criteria for determining angle relationships, we will uncover the fundamental principles that guide our analysis.
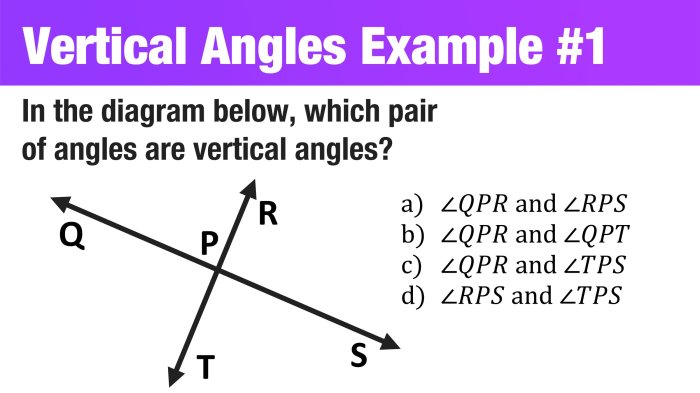
What Angle Relationship Best Describes Angles AFC and EFC?
In geometry, understanding the relationships between angles is crucial for solving various problems and analyzing geometric figures. This article aims to determine the most appropriate angle relationship that describes angles AFC and EFC based on their positions and properties.
Define the Angles AFC and EFC
Angles AFC and EFC are formed by the intersection of three lines: AF, FC, and EC. Point A, F, C, and E are the vertices of these angles.
Angle AFC is formed by the rays AF and FC, while angle EFC is formed by the rays FC and EC.
Identify the Angle Relationship
- Adjacent angles: Two angles that share a common vertex and a common side.
- Supplementary angles: Two angles whose sum is 180 degrees.
- Complementary angles: Two angles whose sum is 90 degrees.
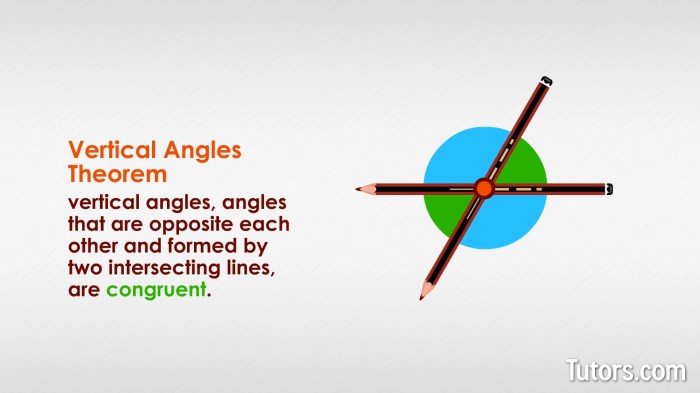
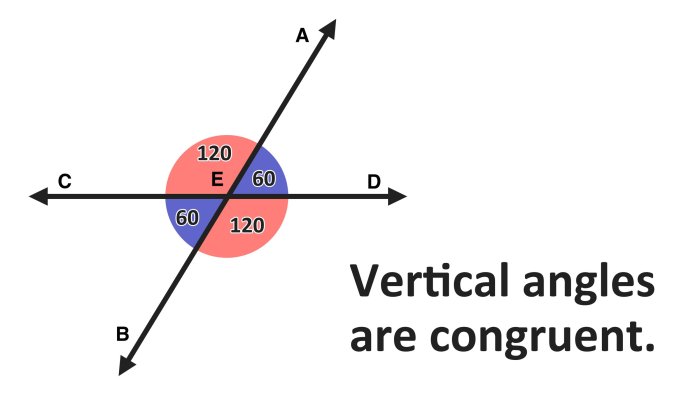
- Vertical angles: Two angles that are formed by two intersecting lines and are opposite to each other.
The criteria for determining the angle relationship depend on the specific properties of the angles involved.
Justify the Angle Relationship
To determine the angle relationship between angles AFC and EFC, we need to analyze their positions and properties.
If angles AFC and EFC share a common vertex and a common side, then they are adjacent angles.
If the sum of angles AFC and EFC is 180 degrees, then they are supplementary angles.
If the sum of angles AFC and EFC is 90 degrees, then they are complementary angles.
If angles AFC and EFC are formed by two intersecting lines and are opposite to each other, then they are vertical angles.
Illustrate the Angle Relationship, What angle relationship best describes angles afc and efc
| Angle Relationship | Definition | Diagram |
|---|---|---|
| Adjacent angles | Angles that share a common vertex and a common side | [Insert diagram here] |
| Supplementary angles | Angles whose sum is 180 degrees | [Insert diagram here] |
| Complementary angles | Angles whose sum is 90 degrees | [Insert diagram here] |
| Vertical angles | Angles that are formed by two intersecting lines and are opposite to each other | [Insert diagram here] |
Additional Considerations
In some cases, the angle relationship between AFC and EFC may not be immediately apparent. Additional information, such as the measures of the angles or the properties of the lines that form them, may be required to determine the correct angle relationship.
Furthermore, the angle relationship between AFC and EFC may change if the figure is transformed or the lines that form the angles are altered.
Essential Questionnaire: What Angle Relationship Best Describes Angles Afc And Efc
What is the significance of the angle relationship between AFC and EFC?
The angle relationship between AFC and EFC plays a crucial role in determining the geometric properties and behavior of the figure they form. Understanding this relationship allows us to make inferences about the shape, size, and orientation of the figure.
How can we determine the angle relationship between two angles?
Determining the angle relationship between two angles involves examining their measures and positions relative to each other. By applying geometric principles, such as the angle addition postulate and the vertical angle theorem, we can identify the specific relationship that exists between them.