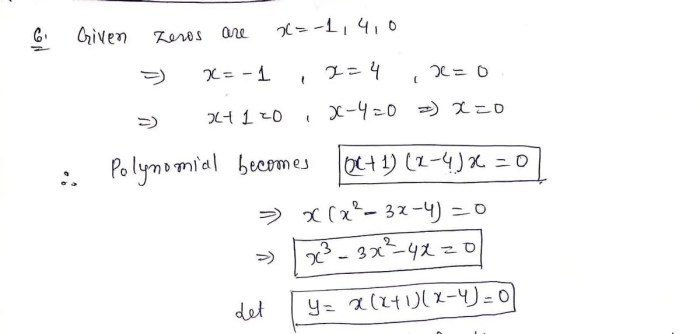Chapter 5 polynomials and polynomial functions – Embarking on a mathematical odyssey, chapter 5 delves into the realm of polynomials and polynomial functions, unveiling their intricate nature and diverse applications. From understanding the fundamental concept of polynomials to mastering operations and exploring their graphical representations, this chapter provides a comprehensive guide to these mathematical powerhouses.
Polynomials, expressions composed of variables and constants, form the foundation of polynomial functions, which represent these expressions in functional form. Through detailed explanations and illustrative examples, this chapter unravels the characteristics of polynomial functions, including their degree, zeros, and end behavior.
1. Introduction to Polynomials: Chapter 5 Polynomials And Polynomial Functions
Polynomials are expressions composed of variables, constants, and mathematical operations, typically addition and multiplication. They represent mathematical functions that have important applications in various fields.
Polynomials are classified based on the number of terms they contain. A monomial has one term, a binomial has two terms, and a trinomial has three terms. Polynomials with more than three terms are called polynomials.
Examples of polynomials include:
- x + 2 (monomial)
- x^2 – 3x + 5 (trinomial)
- x^3 + 2x^2 – 5x + 1 (polynomial)
2. Operations on Polynomials
Polynomials can be manipulated using various algebraic operations. These operations include:
- Addition:Polynomials are added by combining like terms.
- Subtraction:Polynomials are subtracted by changing the sign of the second polynomial and adding it to the first.
- Multiplication:Polynomials are multiplied by multiplying each term of one polynomial by each term of the other polynomial and then adding the products.
- Division:Polynomials can be divided using long division or synthetic division.
For example, to add the polynomials x^2 + 2x + 3 and x – 1, we combine like terms:
x^2 + 2x + 3 + x
- 1 = x^2 + (2x + x) + (3
- 1) = x^2 + 3x + 2
3. Polynomial Functions
A polynomial function is a function that represents a polynomial. It is typically written in the form f(x) = a_nx^n + a_n-1x^n-1 + … + a_1x + a_0, where a_n, a_n-1, …, a_1, and a_0 are constants and n is a non-negative integer.
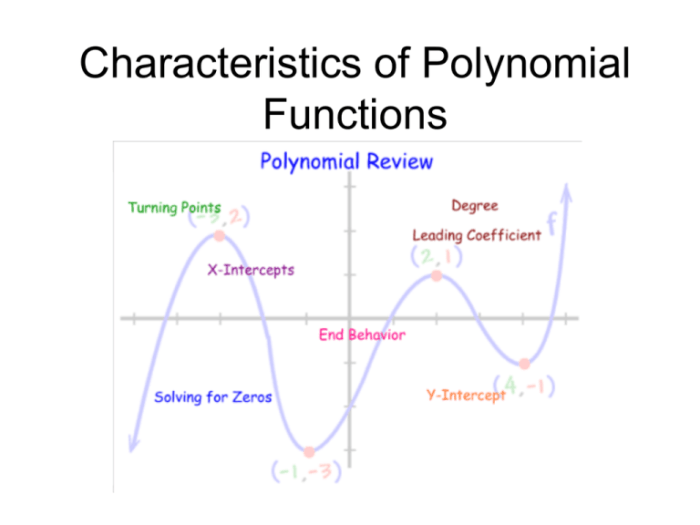
Polynomial functions have several characteristics:
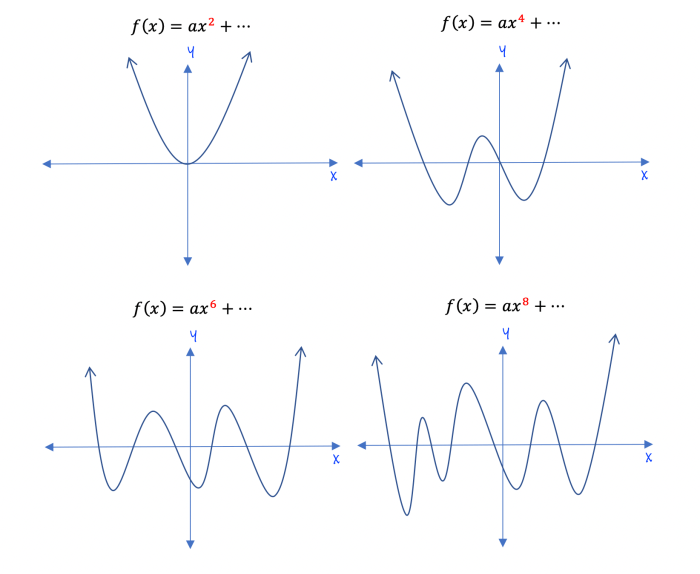
- Degree:The degree of a polynomial function is the highest exponent of the variable.
- Zeros:The zeros of a polynomial function are the values of x for which f(x) = 0.
- End behavior:The end behavior of a polynomial function describes how the graph of the function behaves as x approaches infinity or negative infinity.
4. Applications of Polynomials, Chapter 5 polynomials and polynomial functions
Polynomials have a wide range of applications in various fields:
- Physics:Polynomials are used to model projectile motion, fluid dynamics, and other physical phenomena.
- Engineering:Polynomials are used in structural analysis, control systems, and signal processing.
- Economics:Polynomials are used to model demand curves, production functions, and other economic relationships.
For example, in physics, the trajectory of a projectile can be modeled by the polynomial function h(t) = -0.5gt^2 + vt + h_0, where g is the acceleration due to gravity, v is the initial velocity, t is the time, and h_0 is the initial height.
Query Resolution
What are the different types of polynomials?
Polynomials can be classified into various types based on the number of terms they contain, such as monomials (one term), binomials (two terms), and trinomials (three terms).
How do you perform operations on polynomials?
Polynomial operations involve addition, subtraction, multiplication, and division. Each operation follows specific rules to combine or manipulate polynomial expressions.
What is the significance of the degree of a polynomial function?
The degree of a polynomial function determines its highest exponent and influences its shape, number of zeros, and end behavior.